一致性Hash算法

场景

假如有$3w$张图片，需要缓存到三台服务器上，假设三台服务器编号为01、02、03，我们希望这些图片被均匀缓存到三台服务器上，以便分摊缓存的压力，也就是说，每台服务器大约缓存$1w$张图片。

如果没有任何规律地进行平均分配，可以满足我们的要求（每台服务器缓存压力相同），但是如果要找一张图片时，需要遍历3台服务器。遍历的效率太低，因此不被接受。

应该如何解决这个问题呢？

Hash算法解决

原始的做法：

对缓存项的键进行哈希，将$hash$后的结果对缓存服务器的数量进行取模操作，通过取模后的结果，决定缓存项存在哪台服务器上。举例，假设使用图片名作为访问图片的$key$，假设图片名不重复，则用以下公式进行计算，得到最终存放的服务器编号

$server = hash(Number \: of \: Servers) \: \% \: N$

因为图片名不重复，因此得到的结果是一定的。因此要访问某张图片，只需要按上述公式进行计算，然后去对应的服务器找即可，如果没找到，说明图片没有被缓存，也不用遍历其他服务器了，称这种方法为$Hash$算法。

但是

使用$hash$算法进行缓存时，会出现一些缺陷。

例如，当三台服务器不能满足要求时，需要增加新的服务器进来，但是增加后，服务器的数量发生变化，就需要重新进行一次$hash$计算，在这期间，缓存是失效的；同理，当某台服务器故障时，需要将其移出，则图片缓存的位置必然发生改变，因此以前缓存的图片也会失去缓存的作用和意义，由于大量缓存在同一时间失效，会造成缓存雪崩。

总结一下，普通$hash$算法会出现以下问题：

• 当缓存服务器数量发生变化时，会造成缓存雪崩，引起整个系统压力过大而崩溃？
• 当缓存服务器数量发生变化时，几乎所有缓存的位置都会发生改变，如何减少受影响的缓存？

一致性哈希

基本原理

一致性$hash$也是使用取模的方法，只不过，刚才描述的取模方法是对服务器数量取模，而一致性哈希是对$2^{32}$取模。

首先，将$2^{32}$想像成一个圆，圆的正上方代表$0$，按照顺时针方向，下面的点依次为1、2、3、4...，一直到$2^{32}$，也就是0左边的第一个点为$2^{32}-1$，将这个环称为$Hash$环。

一致性哈希与$Hash$环有什么关系呢？

同样是上面的问题，假设有3台服务器A、B、C，在生产环境中，这三台服务器肯定有自己的$IP$地址，所以我们使用它们各自的$IP$地址进行哈希运算，使用后的结果对$2^{32}$取模，公式为

$server = hash(IP) \: \% \: 2^{32}$

通过以上公式计算出的结果肯定是$0$到$2^{32}-1$中的一个整数，我们就用这个数，代表服务器$A$，由于该整数范围为$0$到$2^{32}-1$，所以上面的$Hash$环上一定有一个点与之对应。

同理，服务器$B$和服务器$C$都可以通过上面的方法映射到$Hash$环上。

到目前为止，三台服务器都可以映射到$Hash$环上。

利用同样的方法，也可以将要缓存的图片的$key$映射到$Hash$环上（图中的点）。

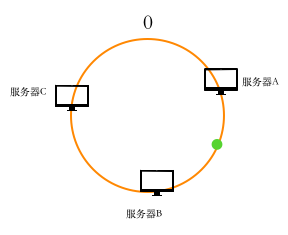
那么上图中，图片应该映射到哪台服务器上呢？我们将点顺时针移动，碰到的第一个服务器即为缓存的服务器，即缓存到服务器$B$上。

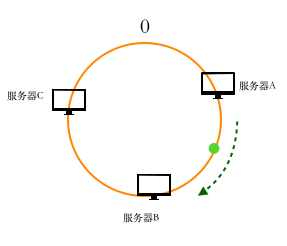
经过上述描述，应该可以明白一致性哈希的原理了。

一致性哈希的优点

但是，一致性哈希能解决先前的问题吗？

当某个节点发生故障时，将该节点进行移除，移除后，缓存到这个服务器的图片会顺应缓存到下一个服务器，但是其他图片不会受到影响，仍然缓存在原来的服务器中，这就是一致性哈希的优点。

如果使用原来的哈希算法，服务器数量发生改变时，所以的服务器缓存都在同一时间失效了，而使用一致性哈希时，只有部分缓存会失效，前端的缓存仍然能分担整个系统的压力，而不至于所有压力都到后端服务器上。

哈希环的倾斜

在理想状态下，三台服务器的位置应该是均匀分布的

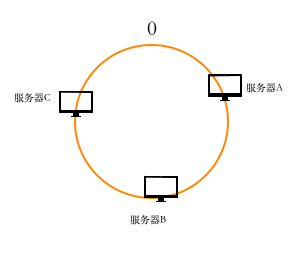
这样的话，缓存会均匀分布在三台服务器上，但实际情况却不一定是这样。

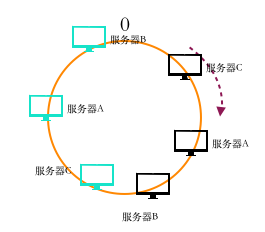
如果出现下面的情况

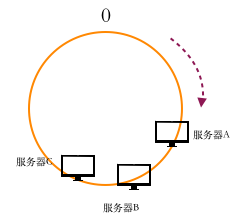
某一台服务器会承担很大的压力，这种情况叫$Hash$环的偏斜。

虚拟节点

如何预防哈希偏斜呢？

就是虚拟出多个节点，一个真实的服务器在哈希环上虚拟出多个位置来

这样的话就可以把环上的空白区域分配给各个节点，而不是全给一个节点，可以抵消哈希环偏斜带来的影响，虚拟节点越多，$hash$环上的节点就越多，缓存被均匀分配的概率就会越大！