Embedding的各向同(异)性

各向同性，在物理上指的是物体在各个方向上的性质相同，比如一个完美的铁圆球，在各个方向上的密度、硬度等等是一样的；各向异性就是在各个方向上性质不同

在Embedding上，各向同性就是向量空间上分布与方向无关，是一致的，而各向异性(Anisotropic)就是在各个方向上的分布不同

一个好的Embedding表示应该满足两点Alignment和uniformity，Alignment表示相似样本间具有相似特征，uniformity表示向量在空间上应该尽量均匀，最好是各向同性的，这样Embedding就可以最大利用向量空间，包含信息最大

参考： https://arxiv.org/pdf/2005.10242.pdf

研究人员通过大量实验发现Transformer结构训练得到的Embedding往往是各向异性的，因此不进行fine-tune的预训练Bert/Gpt/MT5等等直接计算相似文本度（比如cos）往往效果很差，因为各个分量是不正交的（各向异性的），而余弦相似度公式的前提是基底为正交基

解决Embedding的各向异性主要有以下几种方式

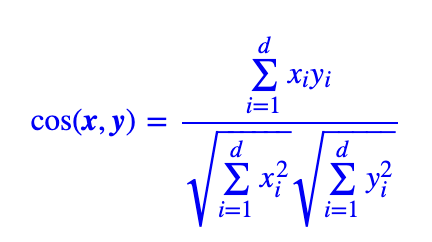
1. 将Embedding映射为各向同性

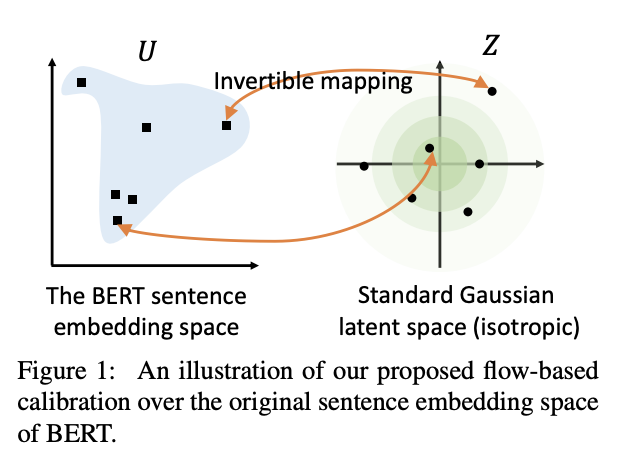
Bert-flow的主要工作就是将原来的Embedding分布映射为高斯分布，标准高斯分布就是各向同性的；

类似的有Bert-whitening，将embedding进行svd分解，旋转缩放后得到标准正太分布

参考：https://kexue.fm/archives/8069

# ****************** 苏神代码 ****************** #

# 单纯白化
def compute_kernel_bias(vecs):
    """计算kernel和bias
    vecs.shape = [num_samples, embedding_size]，
    最后的变换：y = (x + bias).dot(kernel)
    """
    mu = vecs.mean(axis=0, keepdims=True)
    cov = np.cov(vecs.T)
    u, s, vh = np.linalg.svd(cov)
    W = np.dot(u, np.diag(1 / np.sqrt(s)))
    return W, -mu

# 白化+降维
def compute_kernel_bias(vecs, n_components=256):
    """计算kernel和bias
    vecs.shape = [num_samples, embedding_size]，
    最后的变换：y = (x + bias).dot(kernel)
    """
    mu = vecs.mean(axis=0, keepdims=True)
    cov = np.cov(vecs.T)
    u, s, vh = np.linalg.svd(cov)
    W = np.dot(u, np.diag(1 / np.sqrt(s)))
    return W[:, :n_components], -mu

# 应用变换，然后标准化
def transform_and_normalize(vecs, kernel, bias):
    if not (kernel is None or bias is None):
        vecs = (vecs + bias).dot(kernel)
    return vecs / (vecs**2).sum(axis=1, keepdims=True)**0.5

2. 对比学习blabla

详见：Contrastive Learning

References

[1]. On the Sentence Embeddings from Pre-trained Language Models
[2]. Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere