优化器(Optimizer)

目的是为了使网络更快收敛

SGD

分批次进行训练，每次更新反向传播损失

$w_{t+1}=w_t-\alpha g(w_t)$

其中$\alpha$为学习率

• 易受样本噪声影响：如果样本正确可以沿着梯度下降，但是如果样本错误，则可能沿着梯度反方向更新梯度
• 可能陷入局部最优解

SGD+Momentum

$v_t=\eta v_{t-1}+\alpha g(w_t)$

$w_{t+1} = w_t - v_t$

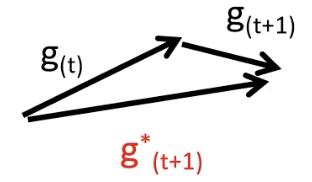
$\alpha$为学习率，$\eta$为动量系数，除了计算当前梯度，还会加上一次的梯度方向，如图所示，可以抑制样本噪声的干扰

Adagrad优化器

$s_t = s_{t-1}+g(w_t)g(w_t)$

$w_{t+1} = w_t - \frac{\alpha}{\sqrt{s_t+\epsilon}}g(w_t)$

$\alpha$为学习率，$\epsilon$为防止分母为零的小数，但是学习率下降太快，可能还没收敛就停止训练了

RMSProp优化器

$s_t = \eta s_{t-1}+(1-\eta)g(w_t)g(w_t)$

$w_{t+1} = w_t - \frac{\alpha}{\sqrt{s_t+\epsilon}}g(w_t)$

在上面的基础上，添加了一个控制衰减系数去调节，防止梯度下降过快。学习率变成了学习率处以二阶动量

Adam优化器

$m_t = \beta_1 m_{t-1}+(1-\beta_1)g(w_t)$

$v_t = \beta_2 v_{t-1}+(1-\beta_2)g(w_t)g(w_t)$

$m_t^{'} = \frac{m_t}{1-\beta_1^t}$

$v_t^{'} = \frac{v_t}{1-\beta_2^t}$

$w_{t+1} = w_t - \frac{\alpha}{\sqrt{v_t^{'}+\epsilon}}m_t^{'}$

$\beta_1,\beta_2$都是控制衰减的系数，添加了一阶动量和二阶动量进行控制