# SVM
# 背景
深度学习(2012)出现之前,SVM被认为是机器学习中最成功的算法。
如果有两类样本点,其实是有很多分割线可以将其分割,那么哪条最优?SVM就是探究这个问题的。
如果两个集合部分相交,如何定义一个超平面,将其大体分开
# 机器学习的一般框架
graph LR
A[训练集] --> B[提取特征向量]
B --> C[结合一定算法 比如决策树 KNN]
C -->D[得到结果]
# SVM介绍
图中有一些点,画一条线把点分成两部分,可以有很多种划分方法,SVM寻找区分两类样本点的超平面(hyper plane),使得margin最大,比如图中的H1、H2、H3。
某些情况下,两类点能被直线很好的区分开,这种情况称为线性可分的,比如上面的例子;在某些情况下,两类点不能被直线分开,只能通过曲线区分开,这种情况称为线性不可分。
# 定义和建立公式
# 最初的想法
对于任意的一个直线划分,可以计算任意一个样本点到直线的距离,可以找到最小的所对应的点,因此目标是让这个距离最近的点离某一条划分线最远(线有无数条,找一条距离最远的)。
注:但是实际上这个是没法做的,因为线有无数条,只是思路是这样的。
# 输入数据
假定存在一个数据集合,类标记为+1和-1,是样本点
注意:logistics回归时,分为0、1,这里的取值没有任何意义,只是为了方便公式推导
# 线性可分支持向量机
给定线性可分训练集,通过间隔最大化得到分离超平面
超平面可以被定义为:
其中是权重,是特征值的个数。根据相应的分类决策函数,可以得到样本类别
如果样本点代入超平面的公式后,值大于0,则分为+1类
样本点代入超平面的公式后,值小于0,则分为-1类
这样就转化为预测值和点代入超平面公式后的乘积总是大于0。
注:实际上是样本点到超平面的距离为正,则乘+1;样本点到超平面为负,则乘-1,不管怎样都大于0,这就是约束!!!
# 目标函数
将最初的想法转换为目标函数:
代入所有样本点,计算最小的距离值,然后求使得距离值最大的分割超平面
重建目标函数,通过调节,使得两类点的函数值都满足,因此距离
新的目标函数为,因为上面距离的最小值就是1,等价改写为求最小值
最终转化为带约束的求极值问题,可以使用拉格朗日乘子法求解!
# 举例
拉格朗日乘子法转化为以下公式

继续计算偏导

将回带到拉格朗日函数中

即转换为当目标函数取最大值时,计算的取值,转化为以下问题

如果得到了这个,则回带得到和,如下所示

举例
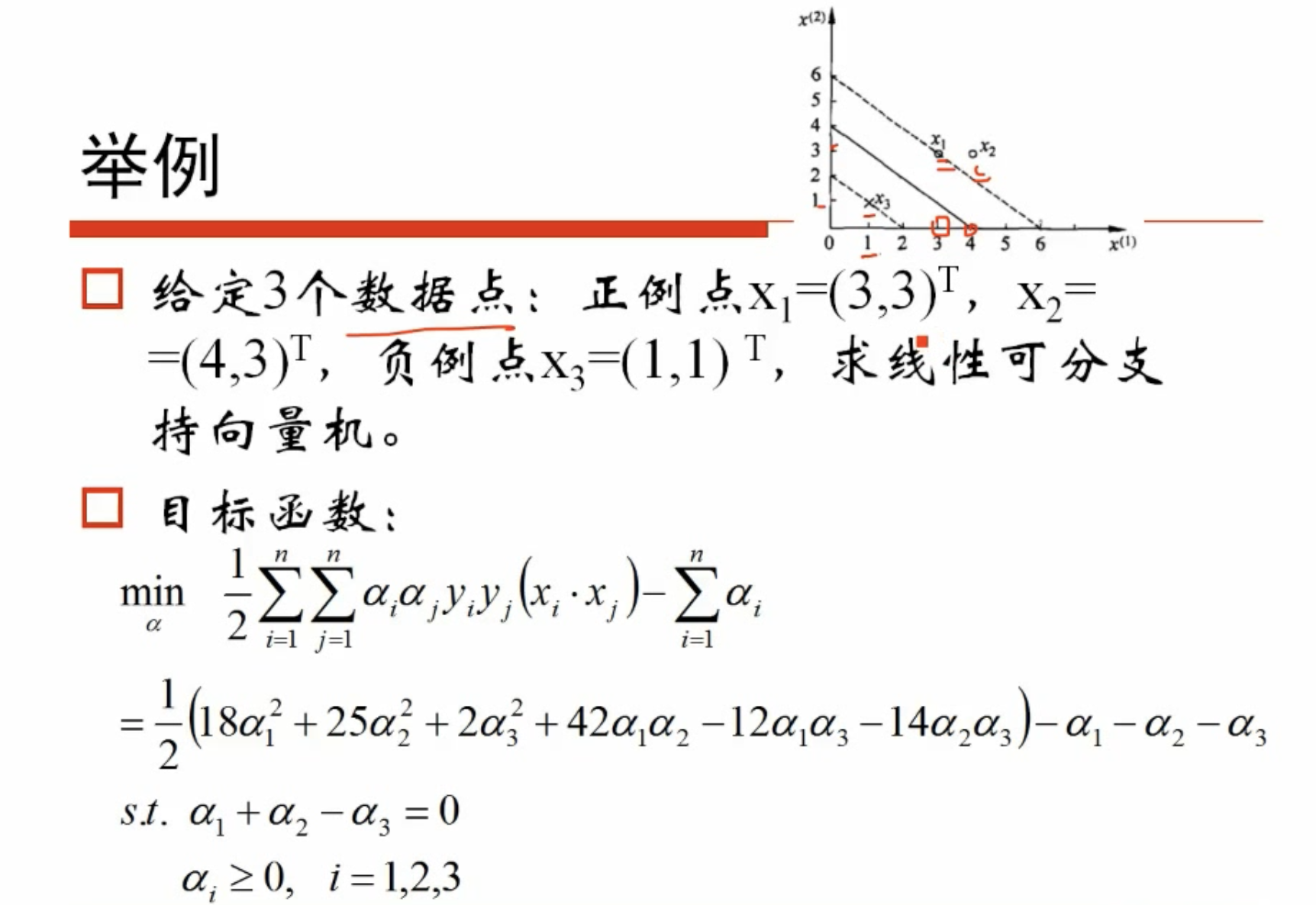
求解二次函数的极值

得到最终超平面

一些样本点对应的可能为0,这对w时没有贡献的(与所有有关),那些不为0的点对应的就是支撑向量
# 总结
# 一些问题
- 不一定分类完全正确的超平面就是最好的,如下图所示
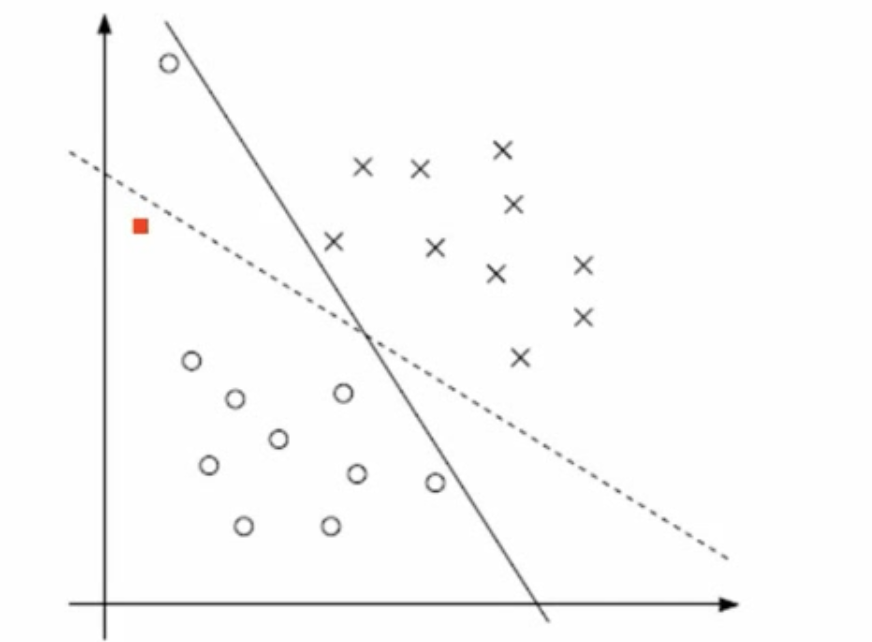
- 样本数据本身线性不可分
因此增加一个松弛因子,不要求严格以1为界,允许某些样本点距离超平面近一点,退化成不是严格线性可分的SVM,这里产生一个超参数C,用于控制松弛因子的影响
C值越大对于训练集的表现越好,但是间隔减小也就是对于噪声等干扰的容忍度减小,可能引发过度拟合(overfitting),这时说明对于噪声的惩罚力度太大
hard-margin是C过大,对于训练集效果更好,对于样本的松弛因子的关注大。这里的目标函数也可以看作是以松弛因子为主,w的L2正则惩罚项来理解


同样用拉格朗日乘子法,做之前相同的操作
# 损失函数
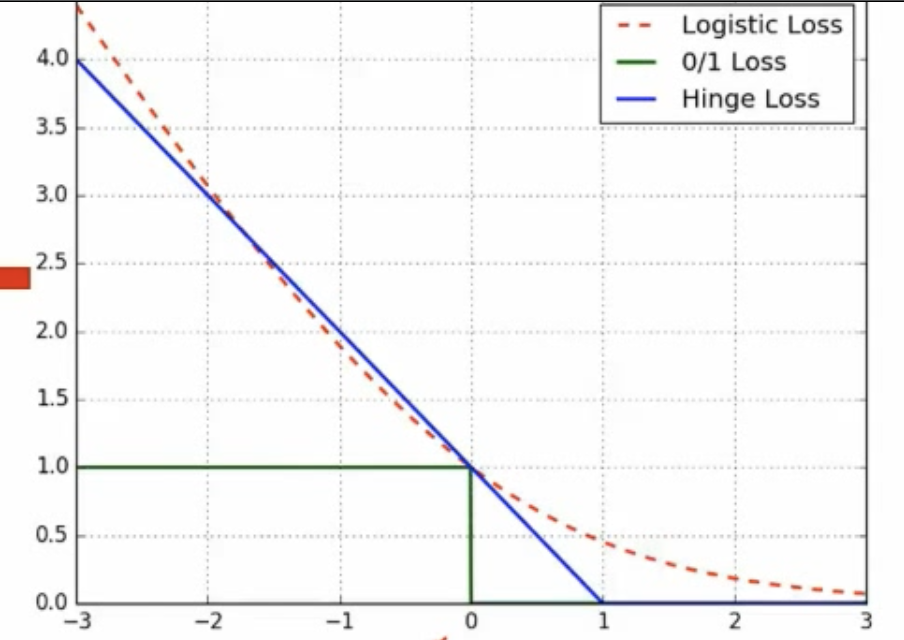
- 0/1损失:如果一类分错了,惩罚就是1,分对了,惩罚就是0
- Logistic损失:,是一个递减的函数
- SVM Hinge(合页)损失:因为假设最小的距离是1,实际上如果落到了距离小于1,那么就给一个损失(分对了,但是落在过渡带区域也有损失
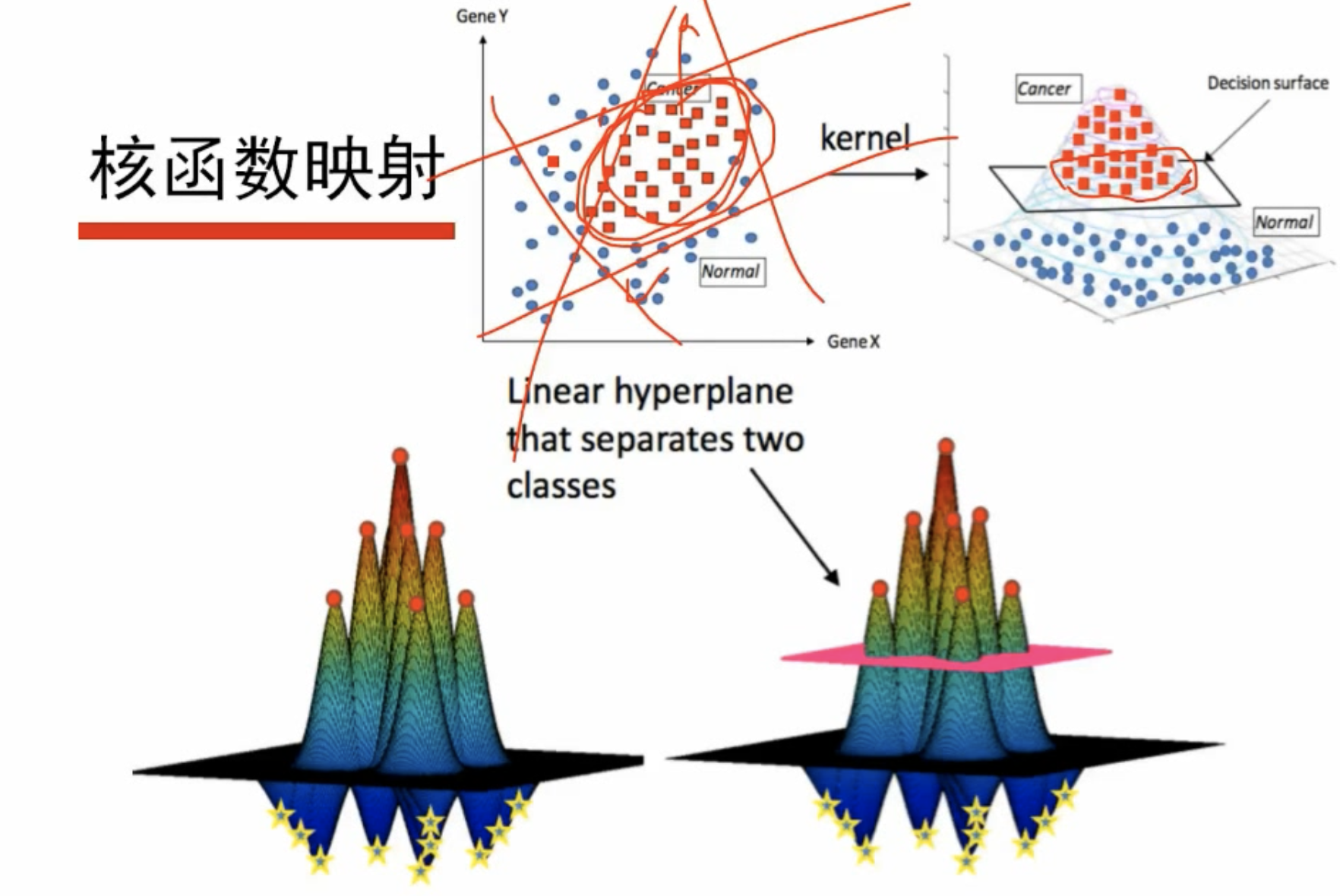
# 核函数

在求解极值的时候,我们并不需要知道两个样本点的特征向量是多少,只需要计算两个样本的点乘值,将这个点乘值定义为核函数K,可以定义一堆核函数,因此绕过了取特征,直接取核就可以

高维空间分割
# 总结与思考

# SVM一些注意点
# SVM原理
存在两类样本数据,尝试在特征空间内用一个超平面对其进行划分,找到一个这样最优的超平面(使得两类样本数据的间隔最大)
- 当两类数据严格线性可分时,可以采用hard-margin使得两类样本点完全分开
- 当两类数据不严格线性可分时,引入一个松弛因子,采用soft-margin使得两类样本点近似线性可分
- 当两类数据非线性可分时,引入核函数,将特征映射到高维空间中,使其在高维空间中线性可分
# SVM为什么采用间隔最大化
将两类数据线性可分时,存在无数个超平面将其划分。SVM利用间隔最大化求得最优的分离超平面,这时的解是唯一的,并且此时分割超平面产生的分类结果是最鲁棒的,对未知实例的泛化能力最强
# 为什么要将SVM的原始问题转换为求解对偶问题
原本是计算所有样本点到超平面的距离,求得到超平面的最小值,然后选择一个合适的超平面,使得这个最小值最大。转换为对偶问题是带约束的凸优化问题,用拉格朗日乘子法进行求解,将目标函数对和求偏导数,将其用表示,最终转化为求关于的极值问题,并且这样可以引入核函数,便于对非线性可分的数据进行处理
# 为什么要引入核函数
如果数据的特征是线性不可分的,就引入核函数,将其映射到高维空间中,使其线性可分,这样不需要求解具体的映射函数,直接引入核函数的公式,便于计算
# 为什么SVM对数据敏感🌟
因为SVM希望样本在特征空间中线性可分,SVM没有处理缺失值的策略,所以特征空间的好坏对SVM的性能至关重要,缺失的特征数据将影响训练结果的好坏
# SVM核函数的区别
一般选择高斯核和线性核。线性核一般用于线性可分的场景,参数少,速度快,一般能满足需要。高斯核用于线性不可分的场景,分类结果依赖参数,寻找最佳参数比较麻烦(可以交叉验证),如果feature数量很大,跟样本差不多,用线性核SVM,如果feature比较小,选择高斯核函数
# 不平衡数据的处理
如果数据不平衡的话,比如一类数据很多,另一类很少。可以将少量的类样本一个较大的权重,也可以更换核函数,从高维进行区分