# 神经网络算法
其中最著名的算法backpropagation(BP算法)
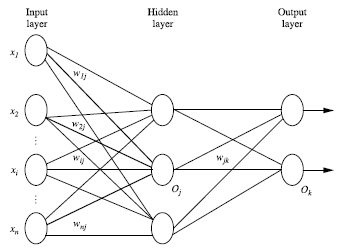
# 多层向前神经网络(Multilayer Feed-Forward Neural Network)
- backpropagation被使用在多层向前神经网络上
- 多层向前神经网络由:输入层、隐藏层、输出层构成
- 每层由单元构成
- 输入层由训练集的实例特征向量传入
- 经过连接节点的权重传入下一层,上一层的输出是下一层的输入
- 每一层进行加权求和,根据非线性方程转化输出
- 作为多层向前神经网络,理论上如果有足够多的隐藏层和足够大的训练集,可以模拟出很多方程
# 设计神经网络结构
- 使用神经网络前,必须确定神经网络的层数以及每层单元的个数
- 特征向量在被传入输入层时通常先被标准化到0——1之间(加速学习过程)
- 离散型变量可以被编码成每一个输入单元对应一个特征值可能赋的值(比如特征值A可以取a,b,c,则可以使用三个特征单元来代表特征值A,如果A=a,那么代表a的单元就取1,否则取0)
- 神经网络可以用作分类和回归问题
- 神经网络用作分类时,如果有两类(比如黑、白),则可以只用一个输出单元进行表示,其中0和1分别代表黑、白,当多于两类的时候,就每一类用一个单元
- 没有明确规则设计隐藏层,需要根据实验测试和误差、以及准确度来实验和改进
# 交叉验证(Cross-Validation)
把数据集分成10份,每次分别取出1份来作为测试集,其他9份作为训练集,然后每次都求出准确度,最后取平均
k-fold cross validation
# BackPropagation算法
- 通过迭代来处理训练集的实例
- 通过对比神经网络后输入层预测值于真实值之间误差。
- 将误差反向传递,传递过程中更新权重和“偏移”两个值,重复这个过程。反方向(输出层=>隐藏层=>输入层)来以最小化误差error更新权重。
# 算法介绍
- 输入:数据集,学习率,一个多层前向神经网络
- 输出:训练好的神经网络
# 初始化权重
初始化weight和bias,随机初始化在-1到1之间,或者-0.5到0.5之间
# 步骤
# 正向输入
图示
对于每个训练实例由输入层输入,然后经过一个激活函数
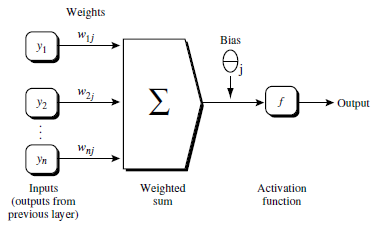
整个过程公式如下
# 根据误差反向传送
对于输出层
对于隐藏层
权重更新
偏向更新
# 终止条件
- 权重低于某个阈值
- 预测的错误率低于某个阈值
- 达到预设的一定循环次数
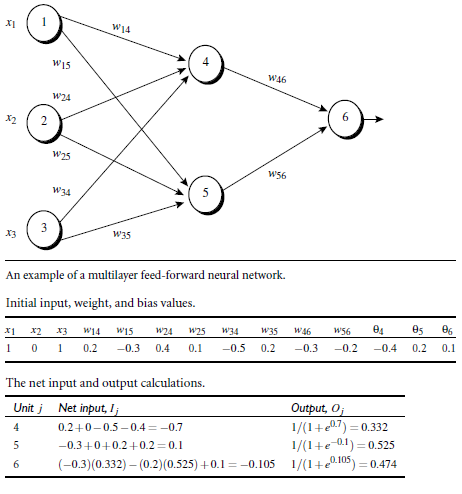
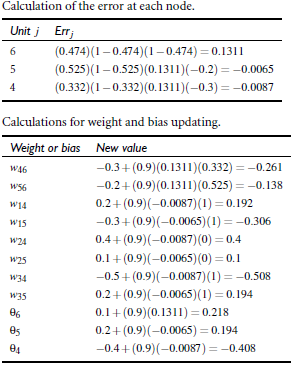
# 例子