# 集成学习

# Boosting

Boosting通过将弱学习器提升为强学习器的集成方法来提高预测精度，典型的是Adaboost、GBDT等

都是由很多弱分类器构成的，每个模型都是欠拟合的

# 加法模型和前向分步

加法模型就是强分类器由一系列若分类器线性相加而成，一般组合形式如下

$F_{M}(x; P) = \Sigma_{m=1}^{n}\beta_{m}h(x;a_{m})$

其中 $h(x;a_{m})$ 是弱分类器， $a_m$ 是弱分类器学习到的最优参数， $\beta_m$ 是弱学习在强分类器中所占的比重， $P$ 是所有 $a_m$ 和 $\beta_m$ 的组合，这些弱分类器线性相加组成强分类器

前向分步是在训练过程中，下一轮迭代产生的分类器是在上一轮的基础上训练得来的，即

$F_m(x) = F_{m-1}(x)+\beta_mh_m(x;a_m)$

# 提升树

提升是每一步产生一个弱预测模型（如决策树），并加权累加到总模型中，如果每一步的弱预测模型生成都是依据损失函数的梯度方向，则称之为梯度提升

通俗举例：一个人30岁，第一次决策树判定20岁，残差是10岁，然后第二棵决策树去拟合这个残差，预测结果是6岁，残差是4岁，然后第三棵树去拟合这个残差...不断迭代，就可以更近似拟合

$f_m = f_{m-1}(x)+T(x,\theta_m)$

上式指的是当前树是上一棵树加上一棵提升树（这棵树的输出结果是上一棵树的残差），相当于

$predict = f_0 + T_1 + T_2 + ... + T_m$

$30 = 20 + 8 + 1 + 0.5 + 0.01 + ...$

关于残差可以直接看作真实值与预测值的差值，也就是损失函数

$L(y, f_N(x)) = y - f_N(x)$

# GBDT

GBDT是回归树，不是分类树
核心在于累加所有树的结果作为最终结果
关键点是利用损失函数的负梯度模拟残差，对于一般的损失函数，只要一阶可导

GBDT是由提升树演变而来的，而提升树可以被认为是Adaboost的一般方法

它的关键点是利用损失函数的负梯度去模拟残差，这样对于一般的损失函数，只需要一阶可导

只需要当前构建的树 $f_m(x)$ 是上一个损失函数的梯度就可以实现，也就是不断求梯度然后加上去就可以，对于平方损失，就是 $y_p - y$ 。

举例：输入原始数据

$D={(x^{1}, y^{1}), (x^{2}, y^{2}) ..... (x^{m}, y^{m})}$

目标使得 $L(y, f(x))$ 最小，其中 $f(x)$ 就是不断生成的GBDT

首先初始化一个数

$f_0(x)=argmin\Sigma L(y_i,f(x_i))$

$f(x_i)$ 指的是输入一个样本 $x_i$ ，分类到某个叶子节点，然后计算这个叶子节点的平均值，也就是数据变为

$D={(x^{1}, r^{1}), (x^{2}, r^{2}) ..... (x^{m}, r^{m})}$

其中 $r$ 就是每个残差

# Adaboost

基本思想是提高前一轮弱分类器错误分类样本的权重，降低正确分类样本的权重，使下一轮分类器更多地去关注那些被分错的样本

Adaboost采用加权投票的方法，分类误差小的弱分类器权重大，分类误差大的弱分类器权重小

# 算法流程

首先初始化样本的权值分布

$D_1 = (w_{1,1}, w_{1,2}, w_{1,3}...w_{1, i}) \ w_{1,i} = \frac{1}{N}, i = 1,2...N$

要训练M个弱分类器
1. 使用具有 $D_m$ 权值分布的训练集进行学习，得到弱分类器 $G_m(x)$
2. 计算 $G_m(x)$ 在你训练数据集上的分类误差率
  e_m = \Sigma_{i=1}^{N}w_{m,i}I(G_m(x_i) \not= y_i)
3. 计算 $G_m(x)$ 在强分类器中的权重
  
  $\alpha_m = \frac{1}{2}log\frac{1-e_m}{e_m}$
4. 更新训练集的权重分布（ $z_m$ 是归一化因子，为了使样本的概率分布和为1）
$w_{m+1,i} = \frac{w_{m,i}}{z_m}exp(-\alpha_my_iG_m(x_i)), i=1,2...10$

$z_m = \Sigma_{i=1}^{N}w_{m,i}exp(-\alpha_my_iG_m(x_i))$
得到最终的分类器是

$F(x) = sign(\Sigma_{i=1}^{N}\alpha_mG_m(x))$

分类器权重的确定后续进行证明

# 损失函数

Adaboost的损失函数是指数损失

$Loss = \Sigma_{i=1}^{N}exp(-y_iF_m(x_i)) = \Sigma_{i=1}^{N}exp(-y_i(F_{m-1}(x_) + \alpha_mG_m(x_i)))$

因为根据前向分步，有

$F_m(x) = F_{m-1}(x)+\alpha_mG_m(x)$

由于进行m轮迭代时，前m-1轮的结果是已知的，因此可以进行化简

$Loss = \Sigma_{i=1}^{N}A_{m,i}exp(-y_i(\alpha_mG_m(x_i)))$

其中 $A_{m,i}=exp(-y_i(F_{m-1}(x)))$ 是每轮迭代的样本权重，而 $F_{m-1(x)}$ 又可以继续向上展开

因此可以得到 $A_{m,i}=A_{m-1,i}exp(-y_i\alpha_{m-1}G_{m-1}(x_i))$

继续化简 $Loss$ ，将其分为预测正确和预测错误的两部分

Loss = \Sigma_{y_i=G_m(x_i)}A_{m,i}exp(-\alpha_m)+\Sigma_{y_i\not=G_m(x_i)}A_{m,i}exp(\alpha_m) = \Sigma_{i=1}^{N}A_{m,i}[\frac{\Sigma_{y_i=Gm(x_i)}A_{m,i}}{\Sigma_{i=1}^{N}A_{m,i}}exp(-\alpha_m) + \frac{\Sigma_{y_i\not=G_m(x_i)}A_{m,i}}{\Sigma_{i=1}^{N}A_{m,i}}exp(\alpha_m)]

公式中，第二项就是分类误差率 $e_m$ ，对Loss进行重写

$Loss = \Sigma_{N}^{i=1}A_{m,i}[(1-e_m)exp(-\alpha_m)+e_mexp(\alpha_m)]$

对 $\alpha_m$ 求偏导数，令其为0，则有

$\alpha_m = \frac{1}{2}log\frac{1-e_m}{e_m}$

即证明了adaboost中每个弱分类器占强分类器的权重

# XGBoost

对目标函数（全部样本Loss的加和）进行了二阶展开，同时用到了一阶和二阶导数，并且添加了正则项，防止过拟合，尽量并发，并且xgboost可以对缺失值处理，将某个特征的缺失值分别放到左子树和右子树，枚举划分点，计算最大的gain，最终确定最大的划分

在建树的过程中，最耗时的是寻找最优的切分点，在这个过程中，最耗时的部分是数据排序，为了减少排序时间，提出了block的结构

block中的数据以稀疏格式csc存储
block中对特征进行排序（不对缺失值排序）
block的特征还需存储指向样本的索引，才能根据特征的值来取梯度
一个block中存储一个或者多个特征值

xgboost的优化函数不是一个连续凸函数，而是一个离散优化问题，优化非常困难，因此采用不同路径，首先将目标函数做一个近似（简化原来的函数，使用泰勒级数），之后将树的结构做一个参数化，通过参数来描述一棵树，之后选一个最优的树，使用贪心算法进行优化

# 目标函数的构建

假设已经训练了k棵树，则第i个样本的预测值为所有树结果的和

目标函数

$Obj = \Sigma_{i=1}^{N} loss(y_i, y_{i_{hat}}) + \Sigma_{j=1}^{t} \Omega(f_j)$

目标函数简单的作为第i个样本的loss加上一个关于树的参数的惩罚项

关于树的复杂度，可以用叶节点的个数和深度等来表征

# 叠加式训练

已知前k-1棵树，构建第k棵树

给定样本 $x_i$ ，在求第k棵树的时候，已经知道k-1棵树，因此，前k-1棵树的输出也已知

目标函数可以简化为：

$Obj = \Sigma loss(y_i, \Sigma y_{(i-1)hat} + f_k(x_i)) + \Sigma \Omega(f_i) + \Omega(f_k)$

$\Sigma loss(y_i, \Sigma y_{(i-1)hat} + f_k(x_i)) + \Omega(f_k)$

# 泰勒级数进一步简化

$f(x+\Delta x) = f(x)+f'(x)\Delta x + 1/2f''(x)\Delta x^2$

将 $loss(y_i,\Sigma y_{(i-1)hat})$ 作为 $f(x)$ ， $f_k(x_i)$ 作为 $\Delta x$ 进行二阶泰勒展开，得到以下公式

$\Sigma [A_if_k(x_i) + B_i f^2_k(x_i)] + \Omega(f_k)$

$A_i, B_i$ 都是常数项，其中 $A_i$ 是每条数据在误差函数上的一阶导数， $B_i$ 是每条数据在误差函数上的二阶导数，是之前的残差，意味着信息的传递

# 新的目标函数

目标是最小化上面的公式，现在的目标就是将位置量进行参数化，因为 $f_k(x_i), \Omega(f_k)$ 肯定是要用具体的参数才能进行优化

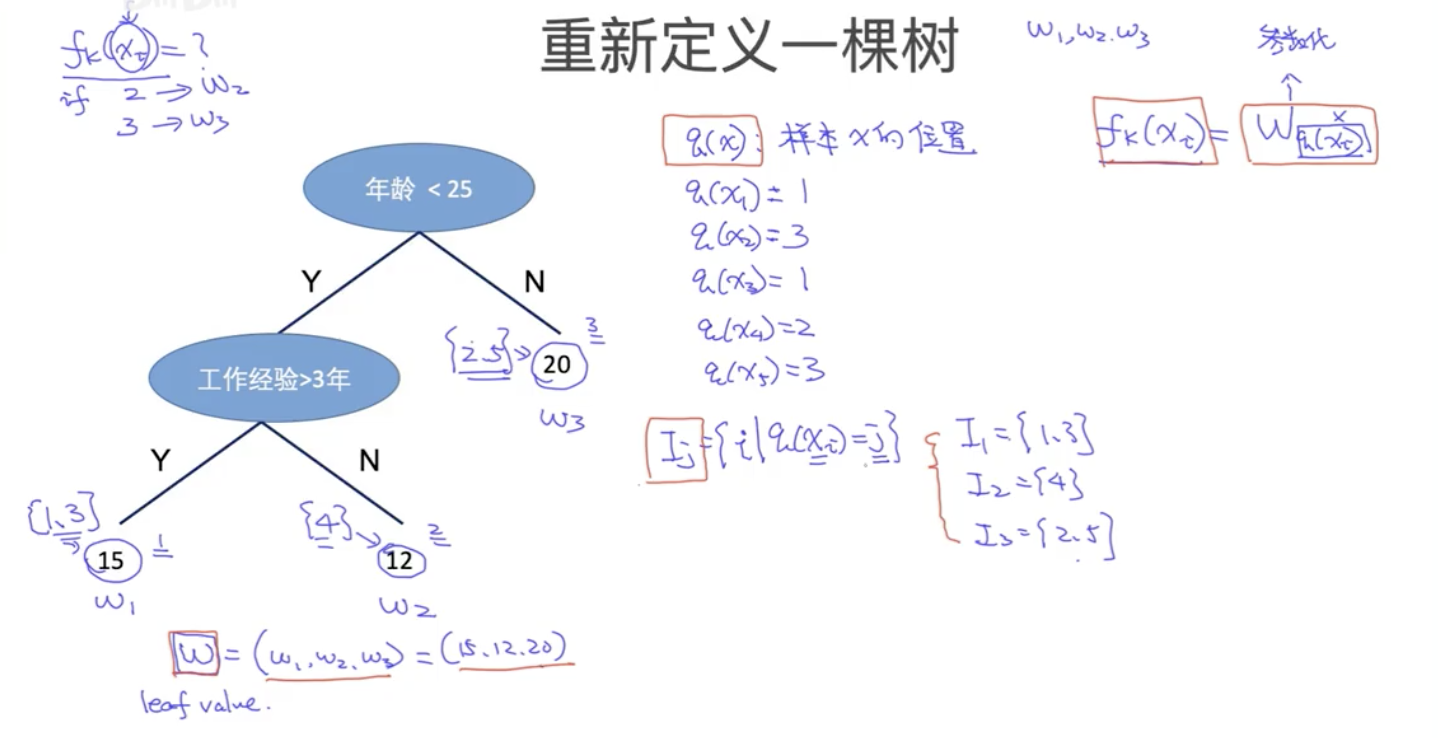
将一棵树的每个叶节点都赋一个权重（也就是每个叶子节点的输出分数），这是第一个参数 $w$
定义一个 $q(x)$ 表示样本 $x$ 的位置，就是某个样本最终落到某个节点的位置

因此 $f_k(x_i)$ 就可以表示为 $w_{q(x_i)}$ ，但是这样在参数下面还有一个参数，很不方便，因此再定义一个参数

$I_j=\{i|q(x_i)=j\}$ ，表示落在 $j$ 号节点的样本集合

然后将复杂度进行参数化， $\Omega f_k = T + \Sigma w^2$ ，一个就是树的叶节点个数，一个是每棵树的叶节点输出分数的平方和（相当于L2正则），各自加一个参数进行控制，最终得到新的目标函数

$Obj = \Sigma [A_i*w_{q(x_i)}+1/2B_i*w^2_{q(x_i)}] + \alpha T+1/2 \gamma \Sigma w^2$

然后将 $q(x_i)$ 进行表示

$Obj = \Sigma_j [\Sigma_{I_j} A_i*w_j + (B_i+\lambda)*w^2_j] + \alpha T$

现在可以简化为 $aw^2_j + bw_j +C$ ，最优的值为

$w^*_j = - \frac{b}{2a} = - \frac{\Sigma A_j}{\Sigma B_j + \lambda}$

带入目标函数，得到最终的Obj，如果知道10000棵树的形状，就可以求出对应的Obj的值，取那个最小的就是最优的树，因此问题转换为寻找树的形状

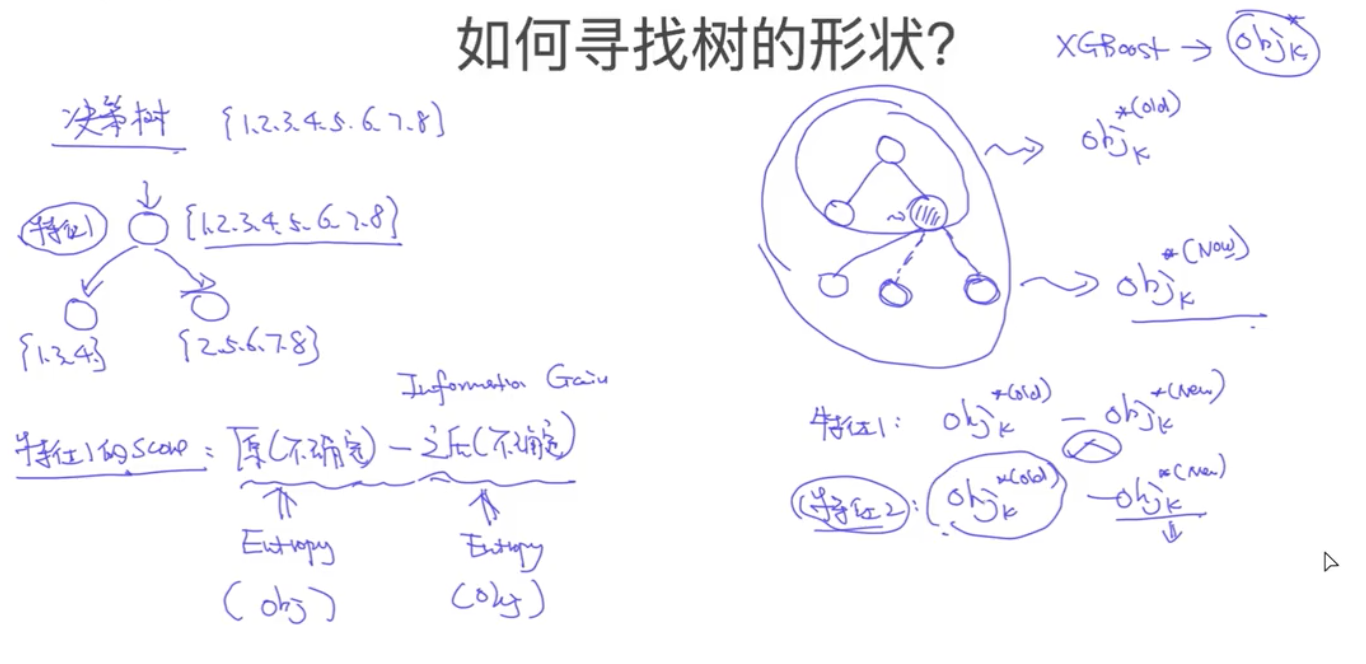
# 寻找树的形状

brute-force search暴力搜索（复杂度太高）

贪心算法，决策树是寻找使得信息增益下降最快的划分，也就是前一棵树和下一棵树的熵的差值

$I(x, y) = H(Y) - H(Y|X)$

在这里将熵改为目标函数的度量即可，也就是对一棵树进行不同特征的继续划分，计算该特征当前的目标函数，下降最快的就是最好的

$Target = Obj^{*old} _k - Obj^{*new}_k$

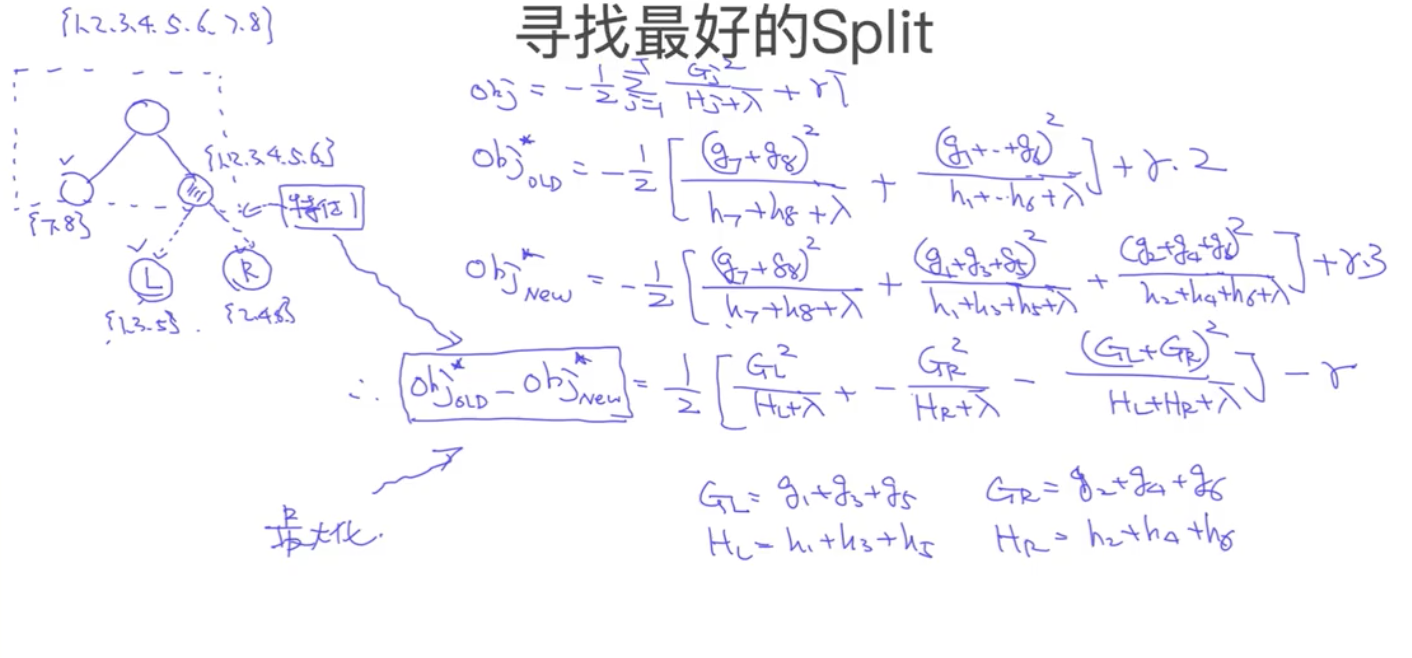
#### 寻找最好的Split

对前一棵树，计算Obj，然后对于某个子节点，依次使用每个特征继续划分，划分后计算对应的Obj，只要找到下降最快的就是最优的（跟决策树的生成一样）

损失函数表示为 $$ Obj = -\frac{1}{2}\Sigma_{j=1}^{T}(\frac{(\Sigma A_j)^2}{\Sigma B_j+\lambda})+\gamma T $$ 因此，$(\frac{(\Sigma A_j)^2}{\Sigma B_j+\lambda})$越大，损失函数越小，可以根据这个值计算增益$Gain$ $$ Gain = \frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_R + H_L+\lambda}] - \lambda $$ 其中第一项为左子树分数，第二项为右子树分数，第三项为分裂前的分数，最后一项为新叶节点复杂度（因为是二叉的所以只会划分左右两个子树）

精确贪心算法

枚举所有特征， $I$ 代表当前节点的数据集， $d$ 表示特征维度
初始化m棵候选树，遍历所有m棵树，将左右子树的一阶梯度和二阶梯度都设为0，将输入进行排序（从小到大排序），进行分裂，遍历所有的分裂方式，计算左右子树的一阶梯度和二阶梯度，然后计算题下 $Gain$ ，遍历完后，增益最大的树就是最优的树结构

假设树高为H，特征数为d，则总的复杂度为 $O(H*d*nlogn)$ ，其中 $nlogn$ 是排序复杂度，因此复杂度比较高

考虑上述算法的近似算法

当数据量庞大，无法全部存入内存中时，精确算法很慢，因此引入近似算法。根据特征k的分布确定l个候选切分点 $S_k = {s_{k1}, s_{k2}, s_{k3} ...s_{kl}}$ ，然后根据候选切分点把相应的样本放入对应的桶中，对每个桶的G、H进行累加，在候选切分点集合上进行精确贪心查找

# Bagging

通过自助采样的方法生成众多并行式的分类器，通过少数服从多数的原则来确定最终结果，典型算法为随机森林

提升的意义：如果一个问题存在若分类器，则可以通过提升的办法得到强分类器

Bagging都是由很多多个弱分类器构成的，每个模型都是过拟合的

← EM算法神经网络算法 →