梯度下降算法

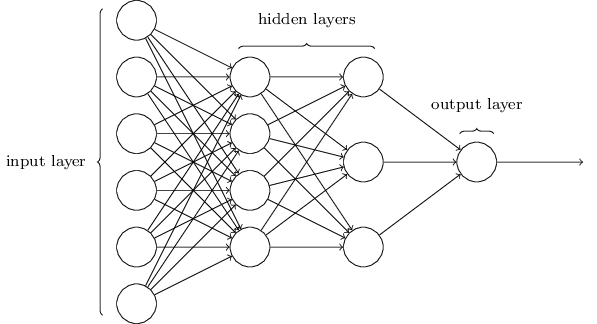
两个隐藏层的神经网络（输入层+隐藏层+输出层），MultiLayer Perceptions（MLP）：实际是sigmoid neurons，不是perceptions（0、1取值）

实例

利用梯度下降算法结合神经网络识别手写数字MNIST数据集：

• 训练数据集：60000张图片
• 测试数据集：10000张图片

输入为每一张图片（28*28）中的784个像素点，每个值代表图片中一个像素值

如果输入的某个图片是数字6，则期待的理想输出应该为

$y(x) = (0,0,0,0,0,0,1,0,0,0)^T:$

目标函数

首先要确定一个目标函数，将代价函数作为目标函数
Cost function（loss function， objective function）目标函数：

$C(w,b) = \frac{1}{2n}\sum_x||y(x)-a||^2$

其中：

• $C:cost$
• $w:weight$权重
• $b:bias$偏向
• $n:$训练集实例的个数
• $x:$输入值
• $a:$输出值
• $||v||:$向量的$length \quad function$

因此需要$C(w,b)$越小越好，输出的预测值和真实值的差距越来越小，因此目标是最小化$C(w,b)$

梯度下降

最小化问题可以用梯度下降（gradient descent）算法解决

核心思想

对于一个单一变量$x$的曲线，要找到这个曲线的最低点的$x_0$坐标，可以从曲线上的任何一点开始，去求曲线在该点的斜率，然后用该点的$x$坐标减去斜率（可以尝试一下，无论是在最低点的左边还是右边，这样都可以不断靠近最低点，因为当$x$大于$x_0$时，斜率是正的；当$x$小于$x_0$时，斜率是负的），在逼近$x_0$的过程中，斜率的值也会不断减少，当达到最低点的时候，斜率正好为零，不会再发生变化，所以用斜率（梯度）来做为迭代过程的调节因子实在是很合适。

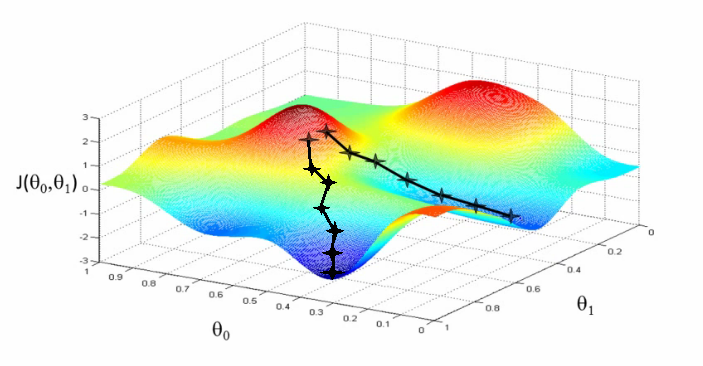
当函数存在多个变量时，构成的是高维的空间曲面，这时同样要去找到这个最低点，如下图所示：

此时，要进行估计$w_k$和$b_l$的值，就需要求偏导数

$w_k \rightarrow w^{'}_{k} = w_k - \eta \frac{\partial C}{\partial w_{k}}$

$b_l \rightarrow b^{'}_{l} = w_k - \eta \frac{\partial C}{\partial b_{l}}$

不断迭代更新权重$weight$和偏向$bias$，最终找到$w$和$b$，使得目标函数最小。

有几点需要注意：

• 最终可能达到局部最优而不是全局最优（与初始点的选取有关）
• 目标函数必须是凸函数（就是碗状的，有最低点）
• 学习率（斜率）会自动减小

梯度是函数最快上升的方向

根据泰勒展开式

$f(x) = f(x_0) + (\theta - \theta_0) \nabla f(\theta_0)$

其中$\theta - \theta_0$代表了步进的信息（包括方向和大小），是一个矢量，因此当从$x_0$前进时，要得到最大的前进值，当且仅当这个前进方向与$\nabla f(\theta_0)$（也就是当前值的梯度方向）相同的时候，此时

$\vec a \cdot \vec b = |a| \cdot |b| cos \theta = |a| \cdot |b|$

取到最大值。（此时两个矢量的方向相同）

因此梯度方向是函数上升最快的方向，梯度方向的反方向是函数下降最快的方向，因此用梯度下降法。