聚类

聚类是对大量位置标注的数据集，按照数据内在的相似性将数据集划分为多个类别，使类别内的数据相似度较大，而类别间的数据相似度较小

给定一个N个对象的数据集，构造k个簇，其中k<N，每个簇至少包含一个对象，每个对象属于一个簇。对于给定的类别k。首先给出初始划分，通过迭代改变样本和簇的隶属关系，使得每一次改进后的划分方案都较前一次好

K-means

有若干个样本，若要分为k个簇

• 选择初始k个类别的中心
• 对于每个样本，将其标记为距离类别中心最近的类别
• 将每个类别中心更新为隶属该类别所有样本的均值（本质是以平方误差作为目标函数时的，梯度下降，如果选择的不是所有样本的，就是随机梯度下降SGD，所有样本的就是批量梯度下降BGD）
• 重复最后两步，直到类别中心的变化小于某个阈值

对k-means的思考

k-means将簇中所有点的均值作为新质心，若簇中含有异常点，将导致均值偏离更严重。比如数据1、2、3、4、100的均值是22，显然100是异常值，因此改成中位数会更稳妥，这种叫$k-Mediods$聚类

对于初值的选择，对聚类结果有影响，初值选择不同，最终的结果也不一定相同。可以根据距离的加权选择聚类中心

使用平方误差作为目标函数，默认了样本服从K个高斯分布的高斯混合分布，因此只能得到类似圆形的聚类区域

最重要的就是K的选取，这决定了最终聚成几个圈

实践中常用交叉验证选取效果最好的

Canopy算法

canopy算法可以归化为聚类算法，使用canopy算法确定聚类的个数$k$，但更多的是可以使用canopy算法做空间索引，器时空复杂度都很出色，算法描述如下

对于给定样本，给定先验值$r1$、$r2$（$r1$<$r2$）

• 所有样本形成列表$L$，每个样本$x_j$都有一个空列表$C_j$
• 随机选择样本$c$，要求$c$的列表为空
• 计算$L$中样本$x_j$与$c$的距离$d_j$
  • 如果$d_j<r_1$，则在$L$中删除$x_j$，将$C_j$赋值为${c}$
  • 否则，将$C_j$增加${c}$
• 如果$L$中没有不满足条件的样本$c$，算法结束

Canopy算法经典介绍

聚类的衡量指标

• 如果一个簇只包含一个类别的样本，则满足均一性
• 同类别样本被归类到相同簇中，则满足完整性

类似于$precision$和$recall$

使用两者的加权平均

轮廓系数（聚类的度量指标）

某个样本属于某个簇，而没有属于其他簇，那就可以计算该样本到同簇的其他样本的距离的平均值，$a_i$越小，就说明这个样本越该被聚类到该簇，$a_i$称为样本$i$的簇内不相似度。

计算样本到其他某簇的所有样本的平均距离$b$，称为样本与其他簇的不相似度，称为簇间不相似度。（$b$越大，说明样本越不属于其他簇）

根据样本的簇内不相似度和簇间不相似度，可以定义轮廓系数

$s(i) = \frac{b(i)-a(i)}{max\{a(i), b(i)\}}$

$s_i$接近1，则说明样本聚类合理，若接近-1，则说明样本更应该分类为其他的簇，若近似为0，说明样本在两个簇的边界上

所有样本的$s_i$的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量

层次聚类

层次聚类对给定数据进行层次的分解，知道满足某种条件为止，具体可以分为

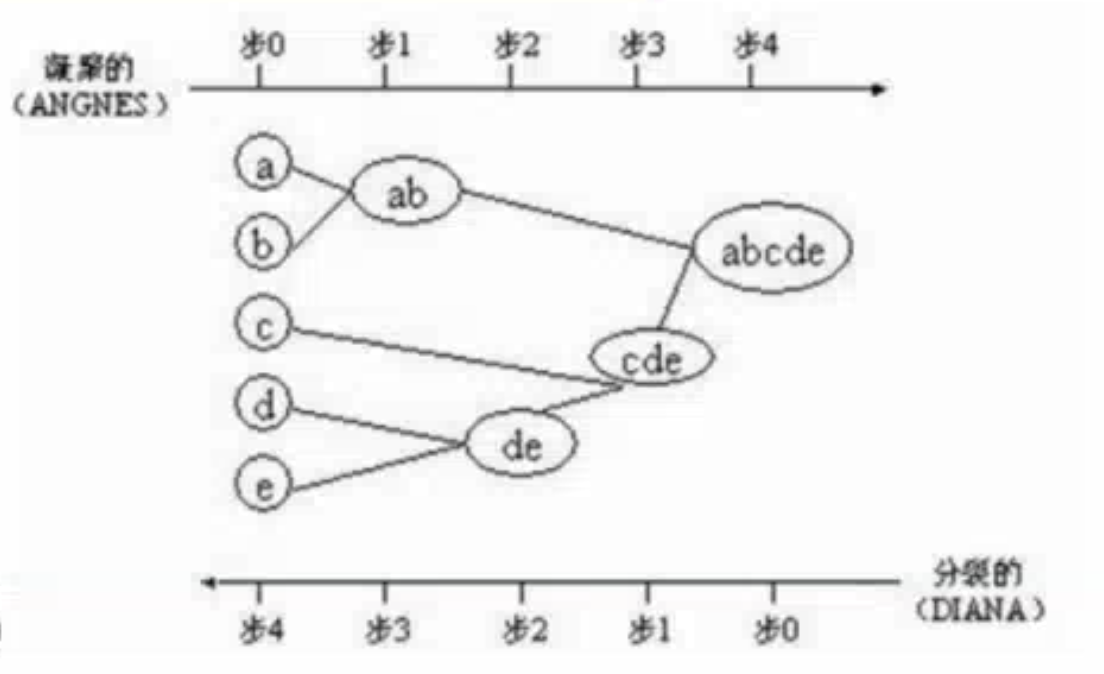
• 凝聚的层次聚类：AGNES算法

  • 一种自底向上的策略，首先将每个对象作为一个簇，然后合并这些原子簇作为越来越大的簇，直到某个终结条件被满足

• 分类的层次聚类：DIANA算法

  • 采用自顶向下的策略，首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇，直到达到某个终结条件

密度聚类

密度聚类的思想是，只要样本的密度大于某个阈值，就将该样本添加到最近的簇中，这种算法能够克服基于距离算法只能发现“类圆形”的聚类缺点，可以发现任意形状的聚类，而且对噪声数据不敏感。但计算密度单元的复杂度高，需要建立空间索引来降低计算量

• DBSCAN（基于空间密度聚类Density-Based Spatial Clustering，允许带噪声Application With Noise）
• 密度最大值算法

DBSCAN

给定一个半径，$\epsilon$邻域。对于给定数目的$m$，如果一个对象的邻域至少包含$m$个对象（周边密度比较高），则称为该对象为核心对象。给定一个对象集合，如果$p$在一个核心对象$q$的邻域内，就说对象$p$从核心对象$q$出发是直接密度可达的。如果$q$直接密度可达$q$，$q$直接密度可达$d$，则说$q$密度可达$d$。如果$p$直接密度可达$q$，直接密度可达$d$，则称$q$和$d$密度相连。一个基于密度的簇是最大密度相连对象的集合。不包含造任何簇中的对象称为噪声。

算法流程

• 如果一个点p密度邻域包含多于m个对象，则创建一个以p为核心对象的新簇
• 寻找并合并核心对象直接密度可达的对象
• 没有新点可以更新簇时，算法结束

因此有如下结果

• 每个簇至少包含一个核心对象
• 非核心对象可以是簇的一部分，构成簇的边缘
• 包含过少对象的簇被认为是噪声

密度最大值聚类

还是定义一个点的邻域，半径为r，在邻域内样本点的个数为这个样本点的局部密度

高局部密度点距离：第i个样本点的局部密度为$\rho_i$，其他点的局部密度为\rho_1、\rho_2...，i个样本点到其他样本点的距离为d_1、d_2...，选择其他样本点$\rho$比$\rho_i$大的作为候选值，在这里面选择距离最小的$d$，这个距离为高局部密度点距离。（在密度高于对象i的所有对象中，到对象i最近的距离，即高局部密度点距离）

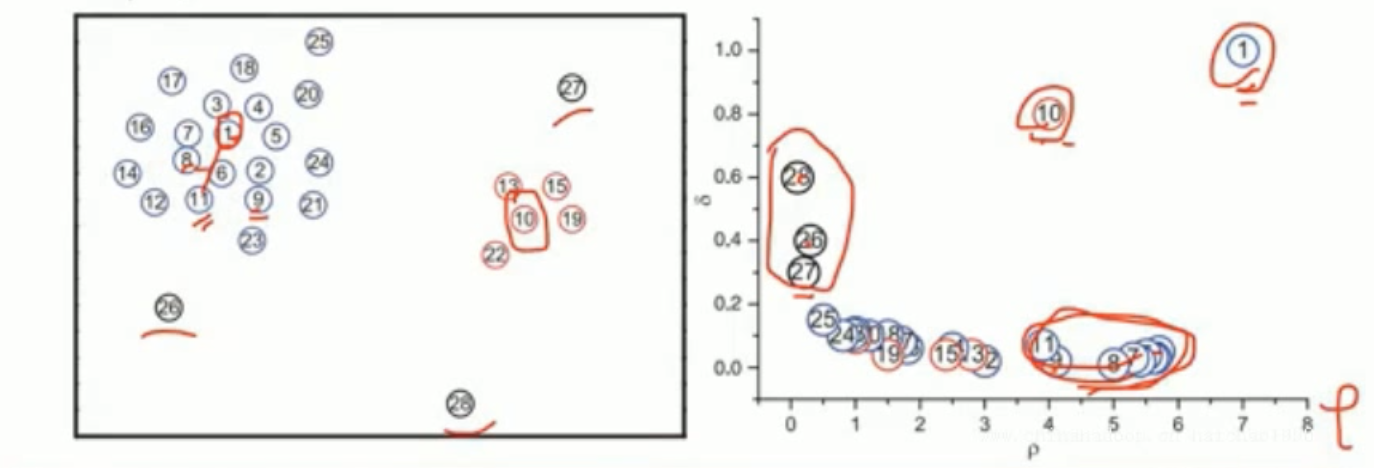
如果一个样本点的局部密度大，高局部密度点距离也比较大，也就是说当前样本点周边聚集着很多样本点，并且距离很远的一个地方，有一个样本点的局部密度比当前样本点更大，就认为这是一个聚类中心

也就是可以将所有样本点的局部密度和高局部密度点距离计算出来，选择都较大的作为聚类中心

谱聚类

方阵作为线性算子，他的所有特征值的全体统称方阵的谱

• 方阵的谱半径是最大的特征值

谱聚类是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据聚类的目的

整体过程

给定一组数据，度量任意两个样本点的相似度，可以形成一个矩阵$W$（相似度矩阵）这个阵如果是高斯相似度的话，是对称的（为了方便计算，将对角线设为0）。 因此某一行的和，就是样本$i$的度（样本i到其他所有样本的距离）。将所有行的和写为一个度矩阵$D(d_1, d_2...)$。通过这两个矩阵$D$和$W$可以得到拉普拉斯矩阵$L$，$L$是对称阵，是半正定的，最小特征值是0，相应的特征向量是全1向量($m$维)

$L = D - W$

如果要求做一个$k$个簇的聚类，就取前$k$个$\lambda$，和对应的特征矩阵（尺寸为mxk），此时认为第$i$个样本的特征就是第$i$行，对其进行聚类，就是对原始数据聚类（谱聚类）的结果

原理上是通过求特征值和特征向量的方式计算出样本的特征，然后再进行$k-means$聚类

还可以使用：对称拉普拉斯矩阵$L=D^{-\frac{1}{2}}LD^{\frac{1}{2}}$、随机游走拉普拉斯矩阵$L=D^{-1}L$