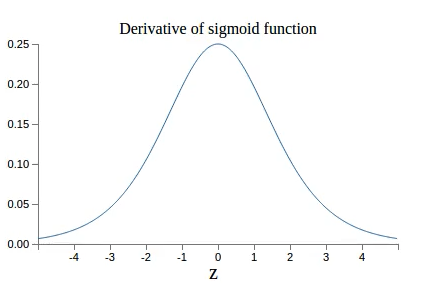
深度神经网络的训练难点

深度神经网络是很多个隐藏层的神经网络，可以学习到不同抽象程度的概念。

例如：图像中，第一层学到边角，第二层学到一些基本形状，第三层学到物体概念。

训练深度学习网络时，不同层的学习率明显不同，接近输出层学习率比较合适，但是前面的层学习太慢，有时会被困住，这个问题被称为消失的$Gradient$问题$(Vanishing \: Gradient \: Problem)$。

理论原因

假设每层只有一个神经元

对于每一级神经元有$z_j = w_ja_{j-1}+b_j$，同时得到$\frac{\partial C}{\partial b_1}$的表达式

$\frac{\partial C}{\partial b_1}=\sigma'(z_1)\times w_2 \times \sigma'(z_2) \times w_3 \times \sigma'(z_4) \times \frac{\partial C}{\partial a_4}$

对$b_1$的一个小变化引起的$C$的变化

$\frac{\partial C}{\partial b_1} \approx \frac{\Delta C}{\Delta b_1}$

如何引起$b_1$的变化

$a_1 = \sigma(z_1) = \sigma(w_1a_0+b_1)$

衡量$z_1$的变化

$\Delta a_1 \approx \frac{\partial \sigma(w_1a_0+b_1)}{\partial b_1}\Delta b_1 = \sigma'(z_1)\Delta b_1$

$a_1$的变化又引起$z_2$的变化，$z_2 = w_2 \times a_1 + b_2$

$\Delta z_2 \approx \frac{\partial z_2}{\partial a_1}\Delta a_1 = w_2\Delta a_1$

把以上$a_1$的变化代入$z_2$的变化

$\Delta z_2 \approx \sigma'(z_1)w_2\Delta b_1$

根据以上规律可以进行推导

$\Delta C \approx \sigma'(z_1)w_2 \sigma'(z_2)...\sigma'(z_4) \frac{\partial C}{\partial a_4}\Delta b_1$

等式两边同时除以$b_1$的变化，得到

$\frac{\partial C}{\partial b_1} = \sigma'(z_1)w_2 \sigma'(z_2)...\sigma'(z_4) \frac{\partial C}{\partial a_4}$

根据上图，$\sigma'$的值小于1/4，$|w|$的值小于等于1，因此在不断连乘的情况下，这个值会不断减小。

解决方法

利用其他激活函数，比如$ReLU$来代替$Sigmod$